08. Color Thresholding
Color Spaces and Thresholding
A color space is a specific organization of colors; color spaces provide a way to categorize colors and represent them in digital images.
RGB is red-green-blue color space. You can think of this as a 3D space, in this case a cube, where any color can be represented by a 3D coordinate of R, G, and B values. For example, white has the coordinate (255, 255, 255), which has the maximum value for red, green, and blue.
Note
: If you read in an image using
matplotlib.image.imread()
you will get an RGB image, but if you read it in using OpenCV
cv2.imread()
this will give you a BGR image.
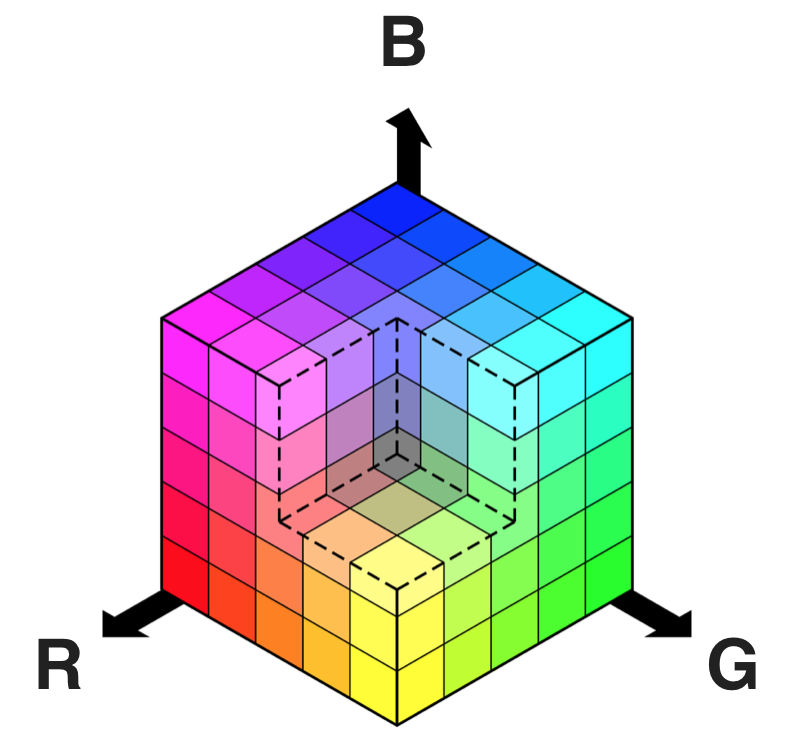
RGB color space
There are many other ways to represent the colors in an image besides just composed of red, green, and blue values.
There is also HSV color space (hue, saturation, and value), and HLS space (hue, lightness, and saturation). These are some of the most commonly used color spaces in image analysis.
To get some intuition about these color spaces, you can generally think of Hue as the value that represents color independent of any change in brightness. So if you imagine a basic red paint color, then add some white to it or some black to make that color lighter or darker -- the underlying color remains the same and the hue for all of these colors will be the same.
On the other hand, Lightness and Value represent different ways to measure the relative lightness or darkness of a color. For example, a dark red will have a similar hue but much lower value for lightness than a light red. Saturation also plays a part in this; saturation is a measurement of colorfulness. So, as colors get lighter and closer to white, they have a lower saturation value, whereas colors that are the most intense, like a bright primary color (imagine a bright red, blue, or yellow), have a high saturation value. You can get a better idea of these values by looking at the 3D color spaces pictured below.
Most of these different color spaces were either inspired by the human vision system, and/or developed for efficient use in television screen displays and computer graphics. You can read more about the history and the derivation of HLS and HSV color spaces here .

(Left) HSV color space, (Right) HLS color space
In the code example, I used HLS space to help detect lane lines of different colors and under different lighting conditions.
OpenCV provides a function
hls = cv2.cvtColor(im, cv2.COLOR_RGB2HLS)
that converts images from one color space to another. If you’re interested in the math behind this conversion, take a look at the equations below; note that all this math is for converting 8-bit images, which is the format for most road images in this course. These equations convert one color at a time from RGB to HLS.
Constants
V_{max} \leftarrow max(R, G, B)
V_{min} \leftarrow min(R, G, B)
These are the maximum and minimum values across all three RGB values for a given color (by pixel).
Note that in these equations, it would be necessary to divide the RGB values by 255 such that they fall in the range
(0, 1)
, but OpenCV will perform this for you in
cv2.cvtColor()
.
L
and
S
are scaled back up after the transformations take place, while
H
is halved for use in 8-bit images (see below).
** H channel conversion equations**
There are three different equations, which one is used depends on the the value of V_{max} whether that's R, G, or B.
\large H \leftarrow \frac{30(G-B)}{V_{max}-V_{min}} , if \: V_{max}=R
\large H \leftarrow 60 + \frac{30(B-R)}{V_{max}-V_{min}} , if \: V_{max}=G
\large H \leftarrow 120 + \frac{30(R-G)}{V_{max}-V_{min}} , if \: V_{max}=B
Note : In OpenCV, for 8-bit images, the range of H is from 0-179. It's typically from 0-359 for degrees around the cylindrical colorspace, but this number is divided in half so that the range can be represented in an 8-bit image whose color values range from 0-255.
** L channel conversion equation**
\large L \leftarrow \frac{V_{max}+V_{min}}{2}
S channel conversion equations
There are two possible equations; one is used depending on the value of L.
\large S \leftarrow \frac{V_{max}-V_{min}}{V_{max}+V_{min}} , if L < 0.5
\large S \leftarrow \frac{V_{max}-V_{min}}{2 - (V_{max}+V_{min})} , if L \geq 0.5